🎓 На цій сторінці ми розберемо 3 правила використання знаку суми.
Якщо ви не знайомі зi знаком суми $\sum$, перейдіть на Що таке знак суми?
-
Правило 1
"Сума константи"
Пояснення на прикладах
\begin{equation}
\sum_{i=\color{red}{k}}^{\color{red}{n}} C=C\cdot (\color{red}{n-k+1})
\end{equation}
Де C будь-який вираз, який не містить індекс сумації "i".
-
Правило 2
"Константу можна винести за знак суми":
Пояснення на прикладах
\begin{equation}
\sum_{i=1}^n \color{blue}{C}\cdot a_i=\color{blue}{C}\sum_{i=1}^n a_i
\end{equation}
\begin{equation}
\sum_{i=1}^n \color{blue}{a_i\pm b_i} =\sum_{i=1}^n \color{green}{a_i} \pm \sum_{i=1}^n \color{green}{b_i}
\end{equation}
Знак суми | Правила та приклади
Наступні правила застосовуються до скінченних сум
(верхня і нижня межі є цілими числами)

В попередніх прикладах ви напевно помітили, що індекс
суми i знаходится внизу знаку
сумації і одночасно зправа напр.: $\sum_{\color{red}{i}=1} ^{5}{\color{red}{i}}$.
Давайте подивимося на
випадок коли індекс суми знаходиться тільки внизу а зправа константа (
вираз в який не входить індекс сумації i ):
$ \sum_{\color{red}{i=1}} ^{\color{red}{2}}{\color{#1299e7}{4}} = 4+4=\color{red}{2}\cdot 4$
Індекс сумації i "йде" від 1 до 2, тому число, що біля суми додається двічі.
🎓 Правило: константу ми додаємо стільки разів скільки є чисел між верхньою і нижньою межами знаку суми включно.
Давайте вирішимо декілька прикладів разом а потім ви самі:
Приклад 1:
$ \sum_{\color{red}{i=1}} ^{\color{red}{3}}{\color{#1299e7}{2}} = ?$
Рішення: тому що i йде від 1 до 3 між нижньою і верхньою межами є 3 числа (1,2,3) - додаємо число біля суми тричі:$ \sum_{i=1} ^{3}{{2}} =2+2+2=3\cdot 2=6$
Приклад 2:
$ \sum_{\color{red}{i=0}} ^{\color{red}{3}}{\color{#1299e7}{2}} =?$
Рішення: тому що i і йде від 0 до 3, тобто ми маємо: 0,1,2,3 ми додаємо двійку чотири рази. Не три (часта помилка).
$ \sum_{i=0} ^{3}{{2}} =2+2+2+2=4\cdot 2=8$
Рішення: тому що i і йде від 0 до 3, тобто ми маємо: 0,1,2,3 ми додаємо двійку чотири рази. Не три (часта помилка).
$ \sum_{i=0} ^{3}{{2}} =2+2+2+2=\\=4\cdot 2=8$
Приклад 3:
$ \sum_{\color{red}{i=4}} ^{\color{red}{8}}{\color{#1299e7}{1}} = ?$
Рішення: i йде від 4 до 8: 4,5,6,7,8. Тобто i набуває пяти значень. Тому ми додаємо 1 пять разів:
$ \sum_{i=4} ^{8}{{1}} =1+1+1+1+1=5\cdot 1=5$
Рішення: i йде від 4 до 8: 4,5,6,7,8. Тобто i набуває пяти значень. Тому ми додаємо 1 пять разів:
$ \sum_{i=4} ^{8}{{1}} =1+1+1+1+1=\\=5\cdot 1=5$
Скільки разів ми додаємо константу? Правило:
Від верхньої межі віднімаємо нижню та додаємо один. На Прикладі 3: 8-4+1=5.
Чому ми додаємо 1? Тому що ми відняли нижню межу 4, але вона має бути включена, адже i набуває 4.
Приклад 4:
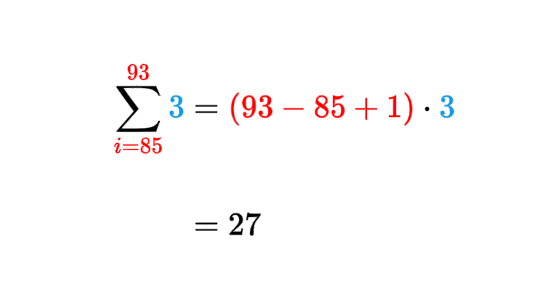
Приклад 5:
Константою може бути будь-що, наприклад Ейфелева вежа 🗼. Головне щоб не було індексу сумації :)
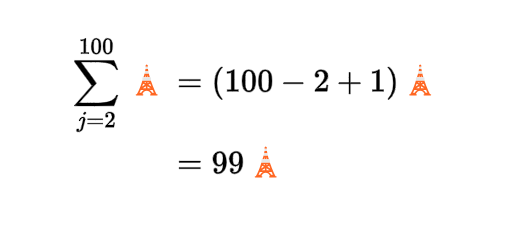
- томущо індекс j (може бути будь яка літера, не тільки i) набуває 99 значень - від 2 до 100.
Тепер приклади для вас, знайдіть суму, якщо біля знаку суми константа:
(рішення можете звірити внизу):
1. $ \sum_{i=1} ^{7}{1}$
2. $ \sum_{i=0} ^{3}{3}$
3. $ \sum_{i=8} ^{25}{4}$
4. $ \sum_{i=5} ^{6}{\frac{1}{2}}$
5. $ \sum_{i=10} ^{22}p$
6. $ \sum_{i=5} ^{25}{0}$
2. Константу можна винести за знак суми
\begin{equation}
\sum_{i=1}^n \color{blue}{C}\cdot a_i=\color{blue}{C}\sum_{i=1}^n a_i
\end{equation}
- подивимося на приклад:
\begin{equation}
\sum_{i=1}^4 \color{blue}{8}\cdot i=
\end{equation}
- тут константа це 8, тому по правилу ми можемо писати:
\begin{equation}
=\color{blue}{8}\sum_{i=1}^4 i \quad ✓
\end{equation}
Пояснення:
розпишемо ліву сторону $\Big(\sum_{i=1}^4 \color{blue}{8}\cdot i\Big)$ і побачимо, що вона дорівнює правій $\Big(\color{blue}{8}\sum_{i=1}^4 i \Big)$:
$\sum_{i=1}^4 \color{blue}{8}\cdot i=\color{blue}{8}\cdot 1+\color{blue}{8}\cdot 2+\\+\color{blue}{8}\cdot 3+\color{blue}{8}\cdot 4=
\\|винесемо \enspace 8\enspace за\enspace дужки|\\
= \color{blue}{8}\cdot (1+2+3+4)\\
| і\enspace запишемо \enspace вираз\enspace \\ в \enspace дужках \enspace за\enspace допомогою\enspace \\ знаку \enspace
суми | \\
= \color{blue}{8}\sum_{i=1}^4 i
$
готово
Порахуємо декілька прикладів разом:
Приклад 6
Використайте Правило 2 та знайдіть суму:
$\sum_{i=5}^{7} 10\cdot (2i+1)= $
|винесемо 10 за знак суми|:
$ =10\sum_{i=5}^{7}(2i+1)=$
|і тепер як завжди|:
$ =10\Big(2\cdot 5+1+2\cdot 6+1+\\ +
2\cdot 7+1\Big)=10\cdot (11+13+15)=\\
=390$
Тепер ваша черга
Винесіть константу за знак суми та додайте:
7) $\sum_{i=1}^3 4\cdot i^2$
8) $\sum_{i=3}^5 \frac{1}{5i}$
Правило 3
\begin{equation}
\sum_{i=1}^n \color{blue}{a_i\pm b_i} =\sum_{i=1}^n \color{green}{a_i} \pm \sum_{i=1}^n \color{green}{b_i}
\end{equation}
- подивимося на приклад:
$\sum_{i=1}^3 \color{blue}{i^2+3} =\sum_{i=1}^3 \color{green}{i^2} +\sum_{i=1}^3 \color{green}{3} \quad ✓$
- вирази в сумі не обов'язково мають містити індекс сумації i (тут число 3).
Пояснення:
розпишемо ліву сторону $\sum_{i=1}^3 \color{blue}{i^2+3}$ і побачимо, що вона дорівнює правій $\Big( \sum_{i=1}^3 \color{green}{i^2} +\sum_{i=1}^3 \color{green}{3}
\Big)$:
Ліва сторона:
$\sum_{i=1}^3 \color{blue}{i^2+3}=(1^2+3)+(2^2+3)+\\
+(3^2+3)=$
|переставимо доданки місцями|
$=(1^2+2^2+3^2)+(3+3+3)=$
|очевидно що цей вираз ми можемо записати як 2 суми:|
=$ \sum_{i=1}^3 \color{green}{i^2} +\sum_{i=1}^3 \color{green}{3} \quad ✓ $
супер, ми показали, що правило працює на цьому прикладі.
Не важко бачити, що воно працюватиме завжди, якщо в межах немає $\pm \infty$. Про це згодом.
Тому з чистою совістю можемо використовувати правило в подальших прикладах :)
Порахуємо разом:
Приклад 7
З використанням правил вище знайдіть суму:
$\sum_{i=2}^{3} 4\cdot i+2= $
|використаємо Правило 3 - розділимо на дві суми: |
$ =\sum_{i=2}^{3} 4\cdot i+\sum_{i=2}^32=$
|в перший сумі винесемо константу 4 за $\sum:$|
$ =4\sum_{i=2}^{3} i+\sum_{i=2}^32=$
|ліву суму порахуємо як завжди, праву як суму константи:|
$4\cdot (2+3)+2\cdot 2=24$
Тепер ви. Використовуючи правила обчисліть суму:
9) $\sum_{i=10}^{11} 2i +3k$
10) $\sum_{i=2}^4 5i -6i^2$
Що якщо в сумі багато чисел, наприклад:
\begin{equation}
\sum_{i=1}^{\color{red}{100}} i ?
\end{equation}
- багато з вас тут впізнає суму арифметичної прогресії. Адже ми додаємо числа від 1 до 100.
- для тих, хто забув :) суму $s_n$ перших n чисел (n натуральне число), ми знаходимо по формулі:
\begin{equation}
s_n= \frac{n}{2}(1+n)
\end{equation}
$s_n$ означає те саме, що i $\sum_{i=1}^n i$
тобто:
\begin{equation}
\begin{split}
\sum_{i=1}^{\color{red}{100}} i &=\frac{100}{2}(1+100)
\\&=5050
\end{split}
\end{equation}
Рішення внизу :]
Рішення
1) $1\cdot 7=7$
2) $4\cdot 3=12$
3) $18\cdot 4=72$
4) $\frac{1}{2}+\frac{1}{2}=1$
5) Скільки разів ми додаємо p? 22-10+1=13 разів.
Відповідь:
$13\cdot p$
6) 0
7) $\sum_{i=1}^3 4i^2=4\sum_{i=1}^3i^2=\\
=4(1^2+2^2+3^2)=54$
8) $\sum_{i=1}^3 \frac{1}{5i}=\frac{1}{5}\sum_{i=1}^3 \frac{1}{i}=\\
=\frac{1}{5}(\frac{1}{1}+\frac{1}{2}+\frac{1}{3})\approx 0.37$
9)
$\sum_{i=10}^{11} 2i +3k=\sum_{i=10}^{11} 2i+\\+\sum_{i=10}^{11} 3k
=2\sum_{i=10}^{11} i+\sum_{i=10}^{11} 3k=\\
\\=2(10+11)+2\cdot 3k=\\
=42+6k
$
3k тут константа
10)
$\sum_{i=2}^4 5i -6i^2=5\sum_{i=2}^4 i -\\ -6\sum_{i=2}^4 i^2
=5(2+3+4)-\\-6(2^2+3^2+4^2)=\\=-1203$