Знак суми $\Sigma$ Сигма | Ні стражданням
В математиці знак суми $\Sigma$ використовується як скорочений запис процесу додавання.
Давайте подивимося на простий приклад в якому ми будемо додавати числа 1, 2, 3:
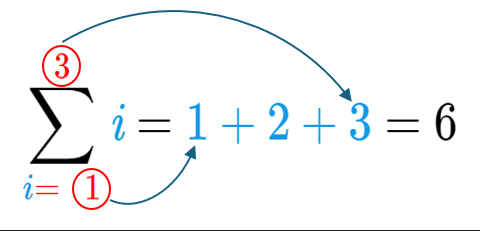
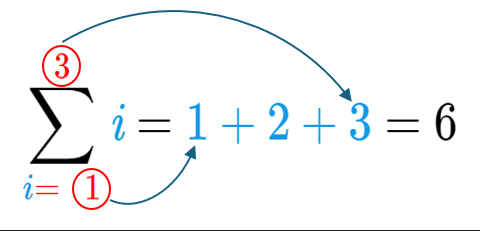
- тобто в "і", що біля суми $\Sigma$,
ми підставляємо числа від одного (i=1 - нижня межа)
до трьох (3 - верхня межа)
і додаємо їх,
трохи формальності:
i - індекс сумації
i=1 - нижня межа сумації: тут починається процес додавання
3 - верхня межа: тут закінчується процес додавання
Давайте подивимося на красу знаку сигма $\sum$! Якщо нам буде дуже терміново потрібно :)) записати суму чисел від одного
до 1000, писати:
1+2+3+...+998+999+1000
було б незручнo
але
але
$ \sum_{i=1} ^{1000}{i}$
елегантно і швидко
Давайте вирішимо декілька прикладів разом а потім ви самі:
Приклад 1:
$ \sum_{\color{red}{i=1}} ^{\color{red}{5}}{\color{#1299e7}{\textit{i}}} = ?$
Рішення: в i ми підставляємо числа від 1 до 5 і додаємо їх:
$ \sum_{i=1} ^{5}{{\textit{i}}} =1+2+3+4+5=15$
Рішення: в i ми підставляємо числа від 1 до 5 і додаємо їх:
$ \sum_{i=1} ^{5}{{\textit{i}}} =1+2+3+4+5=\\=15$
Приклад 2:
$ \sum_{\color{red}{i=1}} ^{\color{red}{3}}{\color{#1299e7}{2\cdot i}} =?$
Рішення: множимо кожне число від одного до трьох на два і додаємо: $ \sum_{i=1} ^{3}{\color{blue}{2}\cdot i} =\color{blue}{2}\cdot1+\color{blue}{2}\cdot2+\color{blue}{2}\cdot3=12$
Рішення: множимо кожне число від одного до трьох на два і додаємо:
$ \sum_{i=1} ^{3}{\color{blue}{2}\cdot i} =\color{blue}{2}\cdot1+\color{blue}{2}\cdot2+\\+\color{blue}{2}\cdot3=12$
Приклад коли нижня межа не дорівнює 1:
Приклад 3:
$ \sum_{\color{red}{i=7}} ^{\color{red}{10}}{\color{#1299e7}{\frac{1}{i}}} =?$
Рішення: підставляємо числа від 7 до 10 і додаємо вирази:
$ \sum_{i=7} ^{10}{\frac{1}{i}} =\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\frac{1}{10}\approx\\ \approx 0.48$
Приклад 4:
$ \sum_{\color{red}{i=3}} ^{\color{red}{5}}{\color{#1299e7}{i-2}} =?$
Рішення: від кожного i віднімаємо 2 і додаємо:
$ \sum_{i=3} ^{5}{i-2} =(3-2)+(4-2)+\\+(5-2)
=5$
Приклад 5:
$ \sum_{\color{red}{i=8}} ^{\color{red}{9}}{\color{#1299e7}{\frac{(-1)^{i}}{i-1}}} =?$
Рішення: просто підставляємо за i і додаємо
$ \sum_{\color{red}{i=8}} ^{\color{red}{9}}{\color{#1299e7}{\frac{(-1)^{i}}{i-1}}}
=\frac{(-1)^8}{8-1}+\frac{(-1)^9}{9-1}=\\
=\frac{1}{7}+\frac{(-1)}{8}\approx 0.018
$
Тепер ваша черга!
Розпишіть і порахуйте суму:
(звірити рішення можете внизу):
1. $ \sum_{i=1} ^{7}{i}$
2. $ \sum_{i=1} ^{5}{3\cdot i}$
3. $ \sum_{i=1} ^{4}{-i}$ :)
4. $ \sum_{i=6} ^{10}{i}$
5. $ \sum_{k=2} ^{5}{\frac{1}{k}}$ - літера може бути будь-якою
6. $ \sum_{k=2} ^{5} k+4$
7. $\sum_{i=2}^3 \frac{(-1)^i}{2i}$
Суму записують також так:
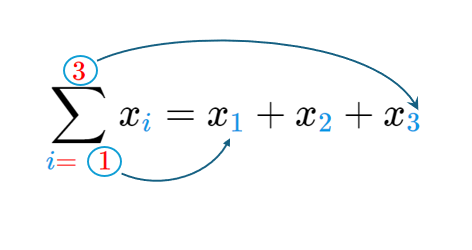
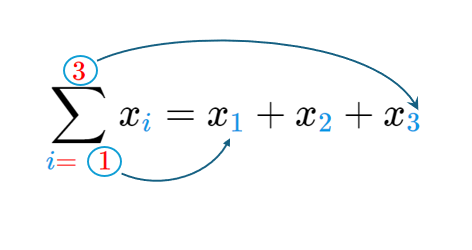
- тобто замість
"і"
ми підставляємо числа від одного
до трьох
і додаємо
- що таке $x_i$? Це зазвичай задано в завданні.
Наприклад: $x_1=7, x_2=5, x_3=11$
Тоді:
\[ \text{$ \sum_{\color{#1299e7}{i} \color{red} {= 1} } ^{\color{red}{3}}x_{\color{#1299e7}{i}} = x_{\color{#1299e7}{1}}
+x_{\color{#1299e7}{2}}+x_{\color{#1299e7}{3}}\\ \enspace \qquad =7+5+11 \\
\enspace \qquad =23 $}
\]
Порахуємо декілька прикладів разом:
Приклад 6:
Нехай $ x_1=10, x_2=-3, x_3=4, $
$x_4=6.$ Знайдіть суму:
$a) \sum_{\color{red}{i=1}} ^{\color{red}{3}}{\color{#1299e7}{\textit{$x_i$}}} = ?$
$b) \sum_{\color{red}{i=2}} ^{\color{red}{4}}{\color{#1299e7}{\textit{$i\cdot x_i$}}} = ?$
Рішення:
a) $\sum_{\color{red}{i=1}} ^{\color{red}{3}}{\color{#1299e7}{\textit{$x_i$}}} =
10-3+4=11 $
b)
Всюди, де є i ми підставляємо числа від 2 до 4 включно і додаємо:
$\sum_{\color{red}{i=2}} ^{\color{red}{4}}{\color{#1299e7}{\textit{$i\cdot x_i$}}} =
2\cdot x_2+3\cdot x_3+ \\ +4\cdot x_4=\\
=2\cdot (-3)+3\cdot 4+4\cdot 6=30 $
І ще один спосіб запису за допомогою знаку суми:
\[ \sum_{\color{#1299e7} {x \in X} }
\color{#1299e7} {x} \]
- означає, що ми додаємо всі x,
які належать (знак "$\in$") до множини X.
Наприклад якщо
x $\in \{1,7,12,9\}$, тоді ми додаємо всі числа з цієї множини:
\[ \sum_{\color{#1299e7} {x \in X} }
\color{#1299e7} {x}= 1+7+12+9=\\=29 \]
Приклад 7:
Нехай $ X=\{2,12,15\}$ Знайдіть суму:
$a) \sum_{x \in X} 3x+1 = ?$
$b) \sum_{x \in X} x^2 = ?$
Рішення:
a) $ \sum_{x \in X} 3x+1= (3\cdot 2+1)+\\+(3\cdot 12+1)
+(3\cdot 15+1)=\\ =7+37+46=90$
b) приклад для вас, перевірити рішення можете внизу (Приклад 8)
Запишіть послідовність за допомогою знаку суми
Тепер обернена задача - записати суму використовуючи знак $\sum$.
Наприклад найпростіший випадок 1+2+3+4 можемо записати так:
$\sum_{i=1}^4 i$
Зверніть увагу, сума не мусить обов'язково починатися з і=1.
Нижня межа може бути наприклад 0, чи будь-яким іншим числом.
Але тоді вираз біля суми мусить бути зміненим так, щоб ми отримали нашу
послідовність 1+2+3+4. Якщо нижня межа буде 0, тоді сума виглядатиме так:
$\sum_{i=0}^3 i+1$. (Перевірте)
Чи 10+11+12 можемо записати:
$\sum _{10}^{12} i$
Як би ви записали за допомогою знаку суми: 15+16+...+21? (відповідь внизу, приклад 9)
Якщо нам треба записати 2+4+6+8+10?
Тут потрібно щоб коли і=1 перше число було 2, коли і=2 друге число було 4 ітд....тобто:
$\sum _{i=1}^{5} 2i$
Як би ви записали: 3+6+9+12? (відповідь внизу, приклад 10)
Чи $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}$ ?
(відповідь внизу, приклад 11)
І останні 2 приклади. Запишіть за допомогою знаку суми:
Приклад 12 :
(-1)+1+(-1)+1+(-1) ?
Приклад 13
$\frac{1}{2}+\frac{2}{3}+\frac{3}{4} ?$
Гортай вниз, але спочатку обчисли сам! :)
Рішення
1) $1+2+3+4+5+6+7=28$
2) $3\cdot 1+ 3\cdot 2+3\cdot 3+3\cdot 4+3\cdot 5=45$
3) $(-1)+(-2)+(-3)+(-4)=-10$
4) $6+7+8+9+10=40$
5) $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}=\frac{77}{60}$
6) $(2+4)+(3+4)+\\+(4+4)
+(5+4)=30$
7) $\frac{(-1)^2}{2\cdot 2}+\frac{(-1)^3}{2\cdot 3}=\\
=\frac{1}{4}+\frac{(-1)}{6}\approx 0.083
$
8) $2^2+12^2+15^2=373$
9) $\sum_{i=15}^{21}i$
10) $\sum_{i=1}^{4}3i$
11) $\sum_{i=1}^{5}\frac{1}{i}$
12) $\sum_{i=1}^{5}(-1)^i$
13) $\sum_{i=1}^3 \frac{i}{i+1}$