Summation index shift
The summation index 'i=1' indicates that the summation begins at one,
with subsequent values plugged into 'i' starting from 1 and incrementing by one each time. Make sure you understand the basics - Summation Notation first.
In some examples, we may want to change the limits (boundaries) of summation.
The terms that we sum must stay the same, so the operation is equivalence.
To better understand, let's look at an example where we will change the boundaries:
\[ \text{$ \sum_{\color{red}{i=1}} ^{\color{red}{3}}{\color{#1299e7}{\textit{i}}} = \color{#1299e7}{1+2+3}$}\]
here we start from 1. Let's say we want to start from 2:
\[ \text{$ \sum_{\color{red}{i=2}}^{?}{\color{#1299e7}{\textit{i}}}=\color{#1299e7}{2+3+4+...}$}\]
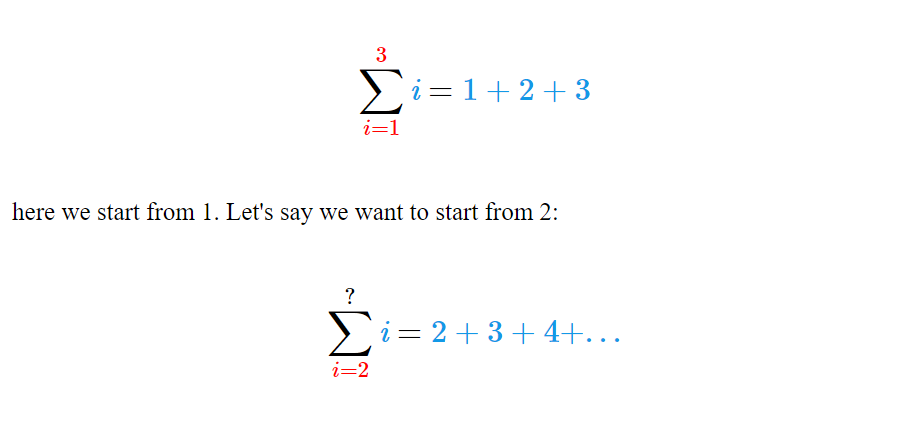
we must keep the summation terms the same as in the first summation!
But now each summation term is greater by one in comparison to
the initial sum. So, we will subtract 1 as follows:
\begin{equation}
\begin{split}
\sum_{\color{red}{i=2}}^{4}\color{#1299e7}{(i-1)} &= \color{#1299e7}{(2-1)+(3-1)+ }\\
& \color{#1299e7}+{\color{#1299e7}{(4-1)}=}\\&=1+2+3
\end{split}
\end{equation}
because we shifted the lower bound from 1 to 2, we also had to shift the upper bound
by one, up from 3 to 4 — so we sum three numbers as before. Done.
From the above, we can conclude that the following equality holds:
\[ \text{$ \sum_{\color{red}{i=1}} ^{\color{red}{3}}{\color{#1299e7}{\textit{i}}} = \sum_{\color{red}{i=2}}^{\color{red}{4}}{\color{#1299e7}{(i-1)}} $}\]
And in general, to shift up by 1:
\[ \text{$ \sum_{\color{red}{i=m}} ^{\color{red}{n}}{\color{#1299e7}{\textit{i}}} = \sum_{\color{red}{i=m+1}}^{\color{red}{n+1}}{\color{#1299e7}{(i-1)}} $}\]

And to shift by any whole number p:
\[ \text{$ \sum_{\color{red}{i=m}} ^{\color{red}{n}}{\color{#1299e7}{\textit{i}}} = \sum_{\color{red}{i=m+p}}^{\color{red}{n+p}}{\color{#1299e7}{(i-p)}} $}\]
where m is any whole number - the lower bound we start from
Let's do more similar examples together, and then you will do a couple on your own.

Example 1: shift summation index up by 1 for:
\[ \text{$ \sum_{k=-1} ^{1}{k} $}\]
Solution: $ \sum_{k=-1} ^{1}{k}=-1+0+1$. Now, let's shift the lower and upper bounds by
one according to the formula above: $ \sum_{k=0} ^{2}{(k-1)=-1+0+1}.$ Great, everything works.
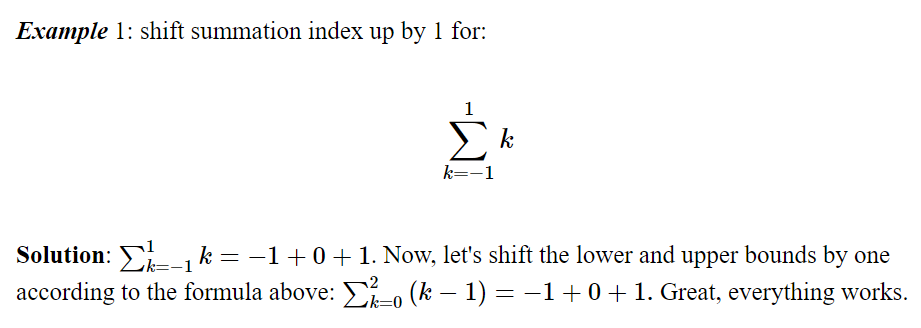
Final solution: $ \sum_{k=-1} ^{1}{k}=\sum_{k=0}^{2}{(k-1)}$
Now it is your turn!
"Student, Example 1":
a) shift the summation index up by 1 for: $ \sum_{i=3} ^{7}{i}$
b) shift the summation index up by 1 for: $ \sum_{i=-2} ^{2}{i}$
you can check solutions at the bottom of this page
Let's continue, Example 2: shift the summation index up by 2 for:
\[ \text{$ \sum_{i=2} ^{3}{i} $}\]
Solution:$ \sum_{i=2} ^{3}{i}=2+3$. Now let's shift lower and upper bounds by
two. Then subtract two from summation variable: $ \sum_{i=4} ^{5}{(i-2)=(4-2)+(5-2)=2+3}.$ Good.
Final solution: $ \sum_{i=2} ^{3}{i}=\sum_{i=4} ^{5}{(i-2})$
Example 3: shift the summation index up by 3 for:
\[ \text{$ \sum_{j=0} ^{2}{(j+1)} $}\]
Solution: we have:

\begin{equation}
\begin{split}
\sum_{j=0}^{2} (j+1) &= (0+1)+(1+1)+\\
& +(2+1)=\\&=1+2+3
\end{split}
\end{equation}
shifting the boundaries by 3 we get:
\begin{equation}
\begin{split}
\sum_{j=0}^{2} (j+1) &= \sum_{j=\color{red}{3}}^{\color{red}{5}} (j+1\color{red}{-3})=\\
& =\sum_{j=3}^{5} (j-2)=\\&=1+2+3
\end{split}
\end{equation}
Final solution: $ \sum_{j=0} ^{2}{(j+1)}=\sum_{j=3} ^{5}{(j-2})$
Now it is your turn!
Solve summation index shift examples (you can check sollutions on the buttom of this page):
Shift the summation index up by 1:
2. $ \sum_{j=10} ^{13}{(j+3)}$
3. $ \sum_{i=3} ^{4}{-i}$
4. $ \sum_{i=-6} ^{-2}{i}$
5. $ \sum_{k=2} ^{5}{2\cdot k}$
Shift the summation index up by 5:
6. $ \sum_{j=1} ^{3}{ j}$
7. $ \sum_{j=1} ^{3}{ 2\cdot j}$
Shift the summation index down by one:
8. $ \sum_{j=1} ^{3}{ j}$
9. $ \sum_{j=11} ^{13}{ (j+4)}$

Solutions are at the bottom on purpose. First, do them yourself :)) and then scroll down.
Solutions
The sums are:
Student Example 1
a) $ \sum_{i=3} ^{7}{i}=\sum_{i=4} ^{8}{(i-1)}$
b)$ \sum_{i=-2} ^{2}{i}=\sum_{i=-1} ^{3}{(i-1)}$
2)
\begin{equation}
\begin{split}
\sum_{j=10}^{13} (j+3)=& \sum_{j=11}^{14} (j+3-1)=\\
& =\sum_{j=11}^{14} (j+2)=\\&=13+14+15+16
\end{split}
\end{equation}
3)
\begin{equation}
\begin{split}
\sum_{i=3} ^{4}{ -i} &= \sum_{i=4} ^{5}{ -(i-1)}=\\
& =\sum_{j=4}^{5} (-i+1)
\end{split}
\end{equation}
4)$ \sum_{i=-6} ^{2}{i}=\sum_{i=-5} ^{3}{(i-1)}$
5)\begin{equation}
\begin{split}
\sum_{k=2}^{5} (2\cdot k) &= \sum_{k=3}^{6} 2\cdot (k-1)=\\
& =\sum_{k=3}^{6} (2\cdot k -2)
\end{split}
\end{equation}
6)$ \sum_{j=1} ^{3}{ j}= \sum_{j=6} ^{8}{ (j-5)}$
7)$ \sum_{j=1} ^{3}2\cdot j= \sum_{j=6} ^{8}{ 2\cdot (j-5)}$
8)$ \sum_{j=1} ^{3}{ j}= \sum_{j=0} ^{2}{ (j+1)}$
9)\begin{equation}
\begin{split}
\sum_{j=11} ^{13}{ (j+4)}&= \sum_{j=10} ^{12}{ (j+4-(-1))}=\\
&=\sum_{j=10} ^{12}{ (j+5)}
\end{split}
\end{equation}